Was ist die Einheit der physikalischen Größe? Kursarbeit: Körperliche Größen und deren Messung
2.2 Einheiten physikalischer Größen
2.3. Internationales VF-System (SI)
2.4. Physikalische Mengen technologischer Prozesse der Lebensmittelproduktion
2.1 Körperliche Größen und Skalen
Körperliche Menge (PV) ist eine der Eigenschaften eines physischen Objekts ( physisches System(Phänomen oder Prozess) ist für viele physische Objekte (physikalische Systeme, ihre Zustände und die in ihnen ablaufenden Prozesse) in qualitativer Hinsicht üblich, in quantitativer Hinsicht jedoch für jedes von ihnen individuell. Das Individuum in quantitativer Hinsicht sollte so verstanden werden, dass dieselbe Eigenschaft für ein Objekt eine bestimmte Anzahl von Malen mehr oder weniger als für ein anderes Objekt sein kann.
In der Regel wird der Begriff "physikalische Größe" auf quantifizierbare Eigenschaften oder Merkmale angewendet. Physikalische Größen umfassen Masse, Länge, Zeit, Druck, Temperatur usw.
Körperliche Größen sollten in unterteilt werden gemessen und ausgewertet.Die gemessene PV kann in Form einer bestimmten Anzahl von festgelegten Maßeinheiten quantifiziert werden. Die Möglichkeit der Einführung und Verwendung der letzteren ist ein wichtiges Unterscheidungsmerkmal der gemessenen EF. Es gibt jedoch Eigenschaften wie Geschmack, Geruch usw., für die keine Maßeinheiten eingegeben werden können. Solche Werte können beispielsweise mit geschätzt werden größenordnung - geordnete Reihenfolge der Werte, die auf der Grundlage der Ergebnisse genauer Messungen angenommen wurden.
Nach Arten von PhänomenenPV ist unterteilt in:
- echtd.h. Beschreibung der physikalischen und physikalisch-chemischen Eigenschaften von Stoffen, Materialien und Produkten. Diese Gruppe umfasst Masse, Dichte, spezifische Oberfläche usw.
energischd.h. Größen, die die Energieeigenschaften der Umwandlungsprozesse, der Übertragung und der Verwendung von Energie beschreiben. Dazu gehören beispielsweise Stromstärke, Spannung, Leistung. Dies sind aktive Größen, die ohne Verwendung von Hilfsenergiequellen in Messinformationssignale umgewandelt werden können.
- den zeitverlauf zu charakterisieren. Diese Gruppe umfasst verschiedene Arten von spektralen Eigenschaften, Korrelationsfunktionen usw.
Von Zugehörigkeit zu verschiedenen Gruppen physischer Prozesse EFs unterteilen sich in Raumzeit, mechanische, thermische, elektrische und magnetische, akustische, Licht-, physikalisch-chemische, ionisierende Strahlung, Atom- und Kernphysik.
Von grad der bedingten Unabhängigkeit von anderen Werten dieser Gruppe EFs unterscheiden sich in Basis (bedingt unabhängig), Ableitungen (bedingt abhängig) und zusätzlich. Grundlegende physikalische Größe - eine physikalische Größe, die in das Mengensystem aufgenommen wird und als unabhängig von anderen Mengen dieses Systems akzeptiert wird. Als die wichtigsten wurden die Werte ausgewählt, die die Haupteigenschaften der materiellen Welt kennzeichnen: Länge, Masse, Zeit. Die verbleibenden vier grundlegenden physikalischen Größen werden so gewählt, dass jede von ihnen einen der Bereiche der Physik repräsentiert: Stromstärke, thermodynamische Temperatur, Materialmenge, Lichtstärke. Jeder physischen Grundgröße eines Quantensystems wird ein Symbol in Form eines Kleinbuchstabens des lateinischen oder griechischen Alphabets zugeordnet: Länge - L, Masse - M, Zeit - T, elektrischer Strom - I, Temperatur - O, Substanzmenge - N, Lichtstärke - J. Symbole sind im Namen eines Systems physikalischer Größen enthalten.
Abgeleitete physikalische Menge - die physikalische Menge, die in das Mengensystem eintritt und durch die Basismengen dieses Systems bestimmt wird. Zum Beispiel ist die Ableitung einer physikalischen Größe die Dichte, definiert durch die Masse und das Volumen des Körpers.
Zusätzliche physikalische Größen umfassen flache und feste Winkel.
Die Kombination aus grundlegenden und abgeleiteten EFs, die nach anerkannten Prinzipien gebildet werden, wird aufgerufen system der physikalischen Größen.
Von anwesenheit der Dimension PV sind in dimensionale unterteilt, d.h. Dimension haben und dimensionslos.
In Fällen, in denen betont werden muss, dass der quantitative Gehalt gemeint ist physikalische Größen In diesem Objekt sollten Sie das Konzept von p verwenden pV-Größe (Größe) ist die quantitative Sicherheit der PV, die einem bestimmten materiellen Objekt, System, Phänomen, Prozess innewohnt.
VF-Wert (Q) - Angabe der Größe einer physikalischen Größe in Form einer bestimmten Anzahl akzeptierter Einheiten. Der Wert der physikalischen Größe wird als Ergebnis einer Messung oder Berechnung erhalten, zum Beispiel 12 kg - der Wert des Körpergewichts.
Der numerische Wert der PV (q) - abstrakte Zahl im Wert enthalten
Gleichung
nannte die grundlegende Messgleichung.
Es gibt einen grundlegenden Unterschied zwischen Größe und Wert. Die Größe hängt nicht davon ab, ob wir es wissen oder nicht. Wir können dieselbe Größe unter Verwendung einer der Einheiten einer gegebenen Größe und eines numerischen Werts ausdrücken (außer für eine Einheit der Masse - kg, zum Beispiel d). Größen verschiedener Einheiten der gleichen Größe sind unterschiedlich.
Die Beziehung zwischen den Basiswerten und den abgeleiteten Werten des Systems wird unter Verwendung der Dimensionsgleichungen ausgedrückt.
Dimension einer physikalischen Größe (dimQ) ist ein Ausdruck in Form eines Potenzmonoms, der die Beziehung zwischen dem Wert und den Basiseinheiten des Systems widerspiegelt und bei dem der Proportionalitätskoeffizient gleich Eins ist. Die Dimension einer Größe ist das Produkt der grundlegenden physikalischen Größen, die auf die entsprechenden Potenzen angehoben werden.
dimQ = L α M β N γ I η (2.2)
wobei L, M, N, I - die Notation des Haupt-PV und α, β, γ, η - reelle Zahlen.
Dimensionalität physikalischer Größen- der Exponent, in dem die Dimension der grundlegenden physikalischen Größe, die in der Dimension der Ableitung der physikalischen Größe enthalten ist, gebildet wird. Dimensionsindikatoren können unterschiedliche Werte annehmen: ganz oder gebrochen, positiv oder negativ.
Der Begriff "Dimension" gilt sowohl für grundlegende als auch für abgeleitete physikalische Größen. Die Dimension der Grundgröße in Bezug auf sich selbst ist gleich Eins und hängt nicht von anderen Größen ab, d. H. Die Formel der Dimension der Grundgröße stimmt mit ihrem Symbol überein, zum Beispiel: Die Dimension der Länge ist L, die Dimension der Masse ist M usw.
Um die Dimension einer Ableitung einer physikalischen Größe in einem bestimmten Quantensystem zu ermitteln, ist es erforderlich, anstelle der Mengenbezeichnung die Dimension der Größen auf der rechten Seite der Definitionsgleichung dieser Größe zu ersetzen. Ersetzen Sie zum Beispiel die Geschwindigkeitsgleichung gleichmäßige Bewegung V = l / t anstelle von dl ist die Abmessung der Länge L und anstelle von dt ist die Abmessung der Zeit T, wir erhalten - dim Q = L / T = LT - 1.
Über Dimensionen kann man die folgenden Aktionen ausführen: Multiplikation, Division, Anhebung einer Potenz und Extraktion der Wurzel.
Dimensionale physikalische Größe - physikalische Größe, in deren Dimension mindestens eine der grundlegenden physikalischen Größen auf eine Potenz erhöht wurde, die nicht gleich Null ist. Wenn alle Exponenten der Dimension der Größen Null sind, wird diese physikalische Größe aufgerufen dimensionslos. Alle relativen Größen sind dimensionslos, d. H. Das Verhältnis von ähnlichen Größen. Beispielsweise ist die relative Dichte r eine dimensionslose Größe. In der Tat ist r = L -3 M / l -3 M = L 0 M 0 = 1.
Der Wert einer physikalischen Größe kann sein wahr, gültig und gemessen. Wirkwert von PV (wahrer Wert einer Größe) ist der Wert einer physikalischen Größe, die qualitativ und quantitativ idealerweise die entsprechende Eigenschaft eines Objekts widerspiegeln würde. Der wahre Wert eines bestimmten Wertes ist vorhanden, er ist dauerhaft und kann mit dem Begriff der absoluten Wahrheit in Verbindung gebracht werden. Es kann nur als Ergebnis eines endlosen Messprozesses mit einer endlosen Verbesserung von Methoden und Messinstrumenten erhalten werden. Für jede Entwicklungsstufe von Messgeräten können wir nur wissen realer Wert der physikalischen Größe- der experimentell ermittelte Wert einer physikalischen Größe, der dem wahren Wert so nahe kommt, dass er sie für die eingestellte Messaufgabe ersetzen kann. Messwert der physikalischen Größe- der Wert einer physikalischen Größe, die mit einer bestimmten Technik erhalten wird.
In der Praxis müssen Messungen verschiedener physikalischer Größen durchgeführt werden. Eine Vielzahl von Ausprägungen (quantitativ oder qualitativ) einer beliebigen Eigenschaft bilden eine Menge, deren Zuordnung zu einer geordneten Menge von Zahlen oder in einem allgemeineren Fall herkömmliche Symbole die Maßstäbe für die Messung dieser Eigenschaften bilden.
Maßstab der physikalischen Größe - ist eine geordnete Menge von PV-Werten, die als Ausgangspunkt für die Messung eines bestimmten Werts dient. Entsprechend der logischen Struktur der Manifestation von Eigenschaften gibt es fünf Haupttypen von Messskalen: Namen, Reihenfolge, Bedingungsintervalle, Beziehungen.
Namensskala (Klassifikationsskala).Solche Skalen werden zur Klassifizierung empirischer Objekte verwendet, deren Eigenschaften sich nur in Äquivalenz äußern, diese Eigenschaften können nicht als physikalische Größen betrachtet werden, daher sind Skalen dieses Typs keine PV-Skalen. Dies ist die einfachste Art der Skalierung, basierend auf der Zuordnung der qualitativen Eigenschaften von Zahlenobjekten, die die Rolle von Namen spielen. In den Namensskalen, in denen die Zuordnung der reflektierten Eigenschaft zu einer bestimmten Äquivalenzklasse unter Verwendung der menschlichen Sinnesorgane das angemessenste Ergebnis ist, das von der Mehrheit der Experten gewählt wird. Gleichzeitig ist die richtige Auswahl von Klassen äquivalenter Klassen von großer Bedeutung - sie müssen von Beobachtern und Experten unterschieden werden, die diese Eigenschaft bewerten. Die Nummerierung von Objekten auf der Namensskala erfolgt nach dem Prinzip: "Weisen Sie unterschiedlichen Objekten nicht dieselbe Nummer zu." Die den Objekten zugewiesenen Zahlen können nur zur Bestimmung der Wahrscheinlichkeit oder Häufigkeit eines bestimmten Objekts verwendet werden. Sie können jedoch nicht für Summierungen oder andere mathematische Operationen verwendet werden. Da diese Skalen nur durch Äquivalenzbeziehungen gekennzeichnet sind, enthalten sie nicht die Begriffe Null, "mehr oder weniger" und Maßeinheiten. Ein Beispiel für Namensskalen sind weit verbreitete Farbatlanten zum Identifizieren von Farben.
Wenn sich eine Eigenschaft eines bestimmten empirischen Objekts in Bezug auf Äquivalenz und Ordnung in der Erhöhung oder Verminderung der quantitativen Manifestation einer Eigenschaft manifestiert, kann sie für sie konstruiert werden maßstab der Reihenfolge. Es nimmt monoton zu oder ab und ermöglicht es, ein mehr / weniger Verhältnis zwischen den Größen festzulegen, die die angegebene Eigenschaft kennzeichnen. In Ordnungsmaßstäben ist Null vorhanden oder nicht vorhanden, jedoch ist es grundsätzlich nicht möglich, Maßeinheiten einzuführen, da für sie keine Proportionalitätsbeziehung besteht und daher nicht beurteilt werden kann, wie oft oder weniger spezifische Ausprägungen einer Immobilie vorliegen.
In Fällen, in denen der Erkenntnisgrad eines Phänomens es nicht erlaubt, die Beziehungen zwischen den Werten eines bestimmten Merkmals genau zu bestimmen, oder die Verwendung einer Skala für die Praxis geeignet und ausreichend ist bedingte (empirische) Skala vonreihe. Dies ist die PV-Skala, deren Ausgangswerte in willkürlichen Einheiten ausgedrückt werden, beispielsweise die Engler-Viskositätsskala, die 12-Punkt-Beaufort-Skala zur Messung der Stärke des Seewindes.
Skalenabstand (Skalenunterschiede sind eine Weiterentwicklung von Ordnungsmaßstäben und werden auf Objekte angewendet, deren Eigenschaften Äquivalenzbeziehungen, Ordnung und Additivität erfüllen. Die Intervallskala besteht aus identischen Intervallen, hat eine Maßeinheit und einen zufällig ausgewählten Anfang, den Nullpunkt. Solche Skalen umfassen die Nummerierung in verschiedenen Kalendern, in denen entweder die Erschaffung der Welt oder die Geburt Christi usw. als Ausgangspunkt genommen wird. Temperaturskalen von Celsius, Fahrenheit und Reaumur sind ebenfalls Intervallskalen.
Beziehungsskala beschreiben die Eigenschaften empirischer Objekte, die die Beziehungen von Äquivalenz, Ordnung und Additivität erfüllen (Skalen der zweiten Art sind additiv) und in einigen Fällen die Proportionalität (Skalen der ersten Art sind proportional). Ihre Beispiele sind die Massenskala (zweite Art) und die thermodynamische Temperatur (erste Art).
In den Beziehungsskalen gibt es ein eindeutiges natürliches Kriterium der quantitativen Null-Manifestation einer Eigenschaft und einer Maßeinheit. Aus formaler Sicht ist die Skala der Beziehungen eine Skala von Intervallen mit einem natürlichen Bezugspunkt. Alle arithmetischen Operationen gelten für die auf dieser Skala ermittelten Werte, was für die Messung der PV wichtig ist. Zum Beispiel kann die Waage der Waage beginnend bei Null unterschiedlich kalibriert werden, abhängig von der geforderten Wiegegenauigkeit.
Absolute Skalen.Unter absoluten Maßstäben zu verstehen, die alle Merkmale von Beziehungsmaßstäben aufweisen, jedoch zusätzlich eine natürlich eindeutige Definition einer Maßeinheit haben und unabhängig von dem verwendeten Maßeinheitssystem sind. Solche Skalen entsprechen relativen Werten: Verstärkung, Dämpfung usw. Für die Bildung vieler abgeleiteter Einheiten im SI-System werden dimensionslose und zählbare Einheiten von absoluten Skalen verwendet.
Beachten Sie, dass Namens- und Reihenfolge-Skalen aufgerufen werden neinmetrik (konzeptionell),und die Skala von Intervallen und Beziehungen - metrik (Material).Absolute und metrische Skalen sind linear. Die praktische Umsetzung von Maßstäben erfolgt durch Standardisierung der Maßstäbe und Maßeinheiten sowie ggf. der Methoden und Bedingungen für deren eindeutige Wiedergabe.
Körperliche Menge (FV) ist eine Eigenschaft, die in der Qualität üblich ist
bezug zu vielen physischen Objekten, jedoch in quantitativer Hinsicht
beziehung zu jedem einzelnen physischen Objekt.
Messung - eine Reihe von Operationen zur Bestimmung
teilen der quantitativen Werte.
Qualitative Eigenschaften von Messwerten . Qualität
charakteristisch für physikalische Größen ist die Größe
ness Es wird durch das aus dem Wort abgeleitete Symbol dim gekennzeichnet
dimension, die je nach Kontext übersetzt werden kann
sowohl als Größe als auch als Dimension.
Messskalen Messskala- es ist ordentlich
eine Menge von Werten einer physikalischen Größe, die dient
grundlage für seine Messung.
Messung Klassifizierung
Messungen können wie folgt klassifiziert werden
1. Zur Erlangung von Informationen:
- gerade linien - dies sind Messungen, bei denen der gewünschte Wert
z-Werte werden direkt erhalten.
- indirekt Ist ein Maß, bei dem die Definition eines
auf der Grundlage des Ergebnisses
direkte Messungen anderer physikalischer Größen, funktionell
aber bezogen auf die gewünschte Menge;
- aggregat - dies sind gleichzeitige Messungen von
wie viele gleichnamige mengen, bei denen der gewünschte Wert liegt
flechtigkeit bestimmt durch Lösen des erhaltenen Gleichungssystems
beim Messen dieser Größen in verschiedenen Kombinationen;
- gemeinsame - Dies sind gleichzeitige Messungen.
zwei oder mehr Mengen desselben Namens zur Bestimmung der
abhängigkeiten zwischen ihnen.
2. Durch die Anzahl der Messinformationen:
Single;
Mehrfach
3. In Bezug auf die Grundeinheiten:
Absolut;
Relativ
4. Nach der Art der Abhängigkeit des Messwerts von der Zeit
statisch;
dynamisch.
5. Abhängig von der physikalischen Beschaffenheit der Messwerte.
messungen sind in Typen unterteilt:
Messung geometrischer Größen;
Messung mechanischer Größen;
Messung der Durchflussparameter, Durchflussmenge, Füllstand, Volumen
Druckmessung, Vakuummessungen;
Messung der physikalisch-chemischen Zusammensetzung und der Eigenschaften von Substanzen;
Thermische und temperaturmessungen;
Messung von Zeit und Häufigkeit;
Messung elektrischer und magnetischer Größen;
Elektronische Funkmessungen
Akustische Messung;
Optische und physikalische Messungen;
Messung der Eigenschaften ionisierender Strahlung und Kernstrahlung
konstanten
Messmethoden
Messmethode - ist ein Trick oder eine Reihe von Tricks
vergleich des Messwertes mit seiner Einheit gemäß
das Prinzip der Messung.
Messprinzip Ist ein physikalisches Phänomen oder ein Effekt
die Basis der Messung. Zum Beispiel das Phänomen der elektrischen
resonanz im Schwingkreis ist die Basis für die Messung
frequenz des elektrischen Signals durch das Resonanzverfahren.
Methoden zur Messung bestimmter physikalischer Größen sind sehr
abwechslungsreich. Im Allgemeinen unterscheiden Sie die Methode des direkten
schätzungen und Vergleichsmethode mit der Maßnahme.
Methode der direkten Bewertung ist dieser Wert
der gemessene Wert wird direkt aus der Referenz ermittelt
gerätemessgerät.
Vergleichsmethode mit Maßzahl besteht darin, dass der gemessene
die Maske wird mit dem von der Messung wiedergegebenen Wert verglichen.
Die Vergleichsmethode mit der Maßnahme weist eine Reihe von Varianten auf. Das ist
widerspruchsmethode, Nullmethode, Substitutionsmethode, Differenzial
mögliche Methode, Übereinstimmungen.
Kontrastmethode ist das messbar
der Betrag und der Betrag, die durch das Maß reproduziert werden, erscheinen gleichzeitig
auf das Vergleichsgerät einwirken, durch das die
die Beziehung zwischen diesen Mengen ist Zum Beispiel
rhenium auf Hebelwaagen mit Ausgleichsgewichten oder
messung der Gleichspannung am Kompensator im Vergleich zu
mit der bekannten EMK eines normalen Elements.
Nullmethode ist das der Nettoeffekt
auswirkung des Messwertes und Messung auf den Vergleicher zu
zu null führen. Zum Beispiel das Messen des elektrischen Widerstands
brücke mit vollem Gleichgewicht.
Substitutionsmethode liegt in der Tatsache, dass die gemessenen
der Rang wird durch ein Maß mit einem bekannten Wert ersetzt. Zum Beispiel
wägen mit alternierender Platzierung der gemessenen Masse und Gewichte
im gleichen Maßstab (Borda-Methode).
Differentialmethode ist das messbar
der Wert wird mit einer homogenen Menge mit einer bekannten verglichen
wert, der geringfügig vom gemessenen Wert abweicht
mengen, und bei denen die Differenz zwischen diesen beiden
nach Mengen. Zum Beispiel Frequenzmessung nach digitaler Frequenz
rum mit heterodyne frequenz träger.
Match-Methode ist das der Unterschied zwischen
messwert und der durch die Messung reproduzierte Wert,
unter Verwendung der Übereinstimmung von Skalenmarkierungen oder periodischen Signalen
bargeld Zum Beispiel Messen der Rotationsfrequenz des Blitzes.
Es muss zwischen der Messmethode und der Leistungsmethode unterschieden werden.
messungen.
Messtechnik - es ist eine etablierte Verbindung
baden von Operationen und Regeln bei der Messung, deren Leistung
liefert Messergebnisse mit Garantie
genauigkeit gemäß der akzeptierten Methode.
Messgeräte
Messgerät (SI) ist ein technisches Werkzeug
für Messungen verwendet und messtechnisch normalisiert
eigenschaften .__
Messen - diese SI soll spielen
physikalische Größe einer bestimmten Größe. Zum Beispiel Gewicht - Maß
masse, Quarzoszillator - ein Maß für die Frequenz, Lineal - ein Maß für die Länge.
Mehrere Maßnahmen:
Stufenlos einstellbar;
Mengen von Maßnahmen;
Geschäfte messen.
Das eindeutige Maß gibt die physikalische Größe von Eins wieder
die Größe.
Ein mehrwertiges Maß gibt eine Reihe von Werten desselben wieder
gleiche physikalische Größe.
Messumformer - das ist SI beabsichtigt
ein Messinformationssignal in der Form zu erzeugen,
bequem für die Übertragung, weitere Konvertierung, aber
vom Bediener nicht nachweisbar.
Messgerät - dieser SI, bestimmt für
signalmessinformationen in einer bequemen Form erzeugen
zur Wahrnehmung durch den Bediener. Zum Beispiel ein Voltmeter, ein Frequenzmesser,
oszilloskop usw.
Messeinrichtung - Diese Kollektion ist funktional
united SI und Hilfsmittel entwickelt
um eine oder mehrere physikalische Größen zu messen und
befindet sich an einem Ort. In der Regel messen
anlagen dienen zur Kalibrierung von Messgeräten.
Messsystem - das Set ist funktionsfähig
united maß messgeräte messen
konverter, Computer und andere technische Mittel
an verschiedenen Stellen des zu kontrollierenden Objekts usw. mit
der Zweck der Messung einer oder mehrerer physikalischer Größen
charakteristisch für dieses Objekt und die Entwicklung von Messsignalen
in verschiedenen ketten. Es unterscheidet sich dadurch vom Messaufbau
die Messinformationen in einer bequemen Form erzeugt
für die automatische Verarbeitung und Übertragung.
Bestimmung der physikalischen Größe
Klassifizierung der physikalischen Größen.
Klassifizierung von Einheiten von physikalischen Größen.
ABSCHNITT 1. METROLOGIE. Thema 3
Thema 3. Physikalische Größen als Messobjekt. SI-System (SI)
Fragen zum Studium:
1. Bestimmung der physikalischen Größe
2. Das internationale System der Einheiten physikalischer Größen SI.
Die physikalische Größe (PV) ist eine Eigenschaft eines physischen Objekts qualit, die für viele Objekte qualitativ ist (dies ist die Art der Menge), aber individuell quantitativ (dies ist die Größe der Menge).
Systemisch - sind in einem der akzeptierten Systeme enthalten (dies sind alle Grundeinheiten, Ableitungen, Mehrfach- und Teileinheiten).
Extrasystem - gehören zu keinem der akzeptierten Systeme von PV-Einheiten (Liter, Seemeile, Karat, PS).
Mehrfach - ϶ᴛᴏ PV-Einheit, deren Wert eine ganzzahlige Anzahl von Malen größer ist als ein System oder eine Nicht-Systemeinheit (z. B. eine Einheit der Länge 1 km = 103m, dh ein Vielfaches eines Meters).
Dolny - ϶ᴛᴏ PV-Einheit, deren Wert eine ganzzahlige Anzahl von Malen ist, die geringer ist als die System- oder Nicht-System-Einheit (z. B. eine Einheit der Länge 1 mm = 10-3m, dh es handelt sich um eine Teileinheit).
Die Grundgrößen hängen nicht voneinander ab und dienen als Grundlage für die Herstellung von Verbindungen zu anderen physikalischen Größen, die als Ableitungen von ihnen bezeichnet werden. In Einsteins Formel zum Beispiel ist E = mc2, Masse ist die Basiseinheit und Energie ist die abgeleitete Einheit.
Die Menge der Basiseinheiten und der abgeleiteten Einheiten wird als Einheitensystem für physikalische Größen bezeichnet. 1960 ᴦ. Das mit SI bezeichnete Internationale Einheitensystem (Systeme International d "Unites) wurde verabschiedet. Es enthält die Basiseinheiten (physikalische Einheiten in Meter, Kilogramm, Sekunde, Ampere, Kelvin, Mol, Candela), zusätzliche und abgeleitete Einheiten (Radiant, Steradiant).
In Wissenschaft, Technik und Alltag beschäftigt sich eine Person mit den verschiedenen Eigenschaften der physischen Objekte um uns herum. Ihre Beschreibung erfolgt anhand physikalischer Größen.
Die physikalische Größe (PV) ist eine Eigenschaft eines physischen Objekts to, die für viele Objekte qualitativ ist (dies ist die Art der Größe - R), jedoch quantitativ individuell (dies ist die Größe der Größe - 10 Ω).
Um für jedes Objekt Unterschiede im quantitativen Inhalt einer durch eine physikalische Größe angezeigten Eigenschaft feststellen zu können, werden die Begriffe seiner Größe und ihres Werts in die Messtechnik eingeführt.
Die Größe der PV ist der quantitative Gehalt in diesem Objekt der Eigenschaft, die dem Konzept der PV entspricht - alle Körper unterscheiden sich in der Masse, ᴛ.ᴇ. von der Größe dieses PV.
Der Wert der PV ist eine Schätzung ihrer Größe in Form einer bestimmten Anzahl von Einheiten, die für sie akzeptiert werden. Es wird als Ergebnis der Messung oder Berechnung von PV erhalten.
Die PV-Einheit ist eine PV mit fester Größe, der üblicherweise ein numerischer Wert gleich 1 zugewiesen wird.
Beispiel: PV - Masse,
die Einheit dieser PV ist 1kᴦ.
wert ist die Masse des Objekts = 5 kᴦ.
Klassifizierung von PV-Einheiten
1. systemisch und nicht systemisch
System - welche in einem der übernommenen Systeme enthalten sind.
* Dies ist die Haupt-, Neben-, Mehrfach- und Teileinheit.
Extrasystem - das in keinem der akzeptierten Systeme von PV-Einheiten enthalten ist:
liter (Volumeneinheit),


liter (Volumeneinheit), Seemeile
karat (Masseneinheit im Schmuckgeschäft e),


karat (Maßeinheit im Schmuckgeschäft e) PS (veraltet)
antriebseinheit)
Die Definition einer physikalischen Größe ist ein Begriff und eine Spezies. Einstufung und Merkmale der Kategorie "Bestimmung einer physikalischen Größe" 2014, 2015.
EINLEITUNG
Die physikalische Größe ist eine Eigenschaft einer der Eigenschaften eines physikalischen Objekts (physikalisches System, Phänomen oder Prozess), die in vieler Hinsicht vielen physischen Objekten gemeinsam ist, jedoch für jedes Objekt quantitativ individuell ist.
Individualität wird in dem Sinne verstanden, dass der Wert einer Menge oder die Größe einer Größe für ein Objekt eine bestimmte Anzahl von Malen mehr oder weniger als für ein anderes Objekt sein kann.
Der Wert einer physikalischen Größe ist eine Schätzung ihrer Größe in Form einer bestimmten Anzahl von Einheiten, die für sie akzeptiert werden, oder einer Anzahl gemäß der für sie verwendeten Skala. Zum Beispiel ist 120 mm ein linearer Wert; 75 kg - der Wert des Körpergewichts.
Unterscheiden Sie zwischen wahren und realen Werten einer physikalischen Größe. Ein wahrer Wert ist ein Wert, der die Eigenschaft eines Objekts perfekt widerspiegelt. Tatsächlicher Wert - der experimentell ermittelte Wert einer physikalischen Größe liegt nahe genug am wahren Wert, der stattdessen verwendet werden kann.
Die Messung einer physikalischen Größe ist eine Menge von Operationen bei der Anwendung einer technischen Vorrichtung, die eine Einheit speichert oder eine Skala einer physikalischen Größe reproduziert, die darin besteht, die Messgröße (explizit oder implizit) mit ihrer Einheit oder Skala zu vergleichen, um den Wert dieser Größe in der für sie günstigsten Form zu erhalten der Verwendung.
Es gibt drei Arten von physikalischen Größen, deren Messung nach grundsätzlich unterschiedlichen Regeln durchgeführt wird.
Die erste Art von physikalischen Größen sind Größen, auf deren Menge von Dimensionen nur die Ordnungs- und Äquivalenzbeziehungen definiert werden. Dies sind Beziehungen vom Typ "weicher", "härter", "wärmer", "kälter" usw.
Werte dieser Art umfassen beispielsweise Härte, definiert als die Fähigkeit eines Körpers, dem Eindringen eines anderen Körpers in ihn zu widerstehen; Temperatur, als Grad der Körperwärme usw.
Die Existenz solcher Beziehungen wird theoretisch oder experimentell mit Hilfe spezieller Vergleichsmittel sowie auf der Grundlage von Beobachtungen der Ergebnisse der Auswirkung einer physikalischen Größe auf beliebige Objekte festgestellt.
Bei der zweiten Art physikalischer Größen findet das Verhältnis von Ordnung und Äquivalenz sowohl zwischen Größen als auch zwischen Paaren ihrer Größen statt.
Ein typisches Beispiel ist der Zeitrahmen. Daher werden Unterschiede in den Zeitintervallen als gleich betrachtet, wenn die Abstände zwischen den jeweiligen Markierungen gleich sind.
Der dritte Typ besteht aus additiven physikalischen Größen.
Additive physikalische Größen sind Größen, auf deren Dimensionen nicht nur die Ordnungs- und Äquivalenzbeziehungen definiert sind, sondern auch Additions- und Subtraktionsoperationen
Diese Werte umfassen beispielsweise Länge, Masse, Stromstärke usw. Sie können in Teilen gemessen und mithilfe einer mehrwertigen Messung basierend auf der Summierung einzelner Messungen reproduziert werden.
Die Summe der Massen zweier Körper ist die Masse eines solchen Körpers, die bei gleichen Schultergewichten durch die ersten beiden ausgeglichen wird.
Die Größen von zwei homogenen PVs oder von zwei beliebigen Größen derselben PV können miteinander verglichen werden, das heißt, Sie können feststellen, wie viele Male größer (oder kleiner) als die anderen sind. Um die m Größen Q ", Q", ..., Q (m) miteinander zu vergleichen, ist es notwendig, ´ m 2 ihrer Beziehungen zu berücksichtigen. Es ist einfacher, jede von ihnen mit der gleichen Größe [Q] einer einheitlichen PV zu vergleichen, wenn wir sie für eine PV-Einheit (in abgekürzter Form - für eine PV-Einheit) nehmen. Als Ergebnis dieses Vergleichs erhalten wir die Ausdrücke für die Größen Q ", Q", ..., Q (m) in Form einiger Zahlen n ", n", ... n (m) Einheiten von PV: Q "= n" [Q]; Q = n [Q]; ... Q (m) = n (m) [Q]. Wenn der Vergleich experimentell durchgeführt wird, sind alle m Experimente erforderlich (anstelle von C m 2), und ein Vergleich der Größen Q ", Q", ..., Q (m) untereinander kann nur durch Berechnung des Typs durchgeführt werden
wobei n (i) / n (j) abstrakte Zahlen sind.
Gleichheitstyp
wird als grundlegende Messgleichung bezeichnet, wobei n [Q] der Wert der Größe der PV ist (abgekürzt als Wert der PV). Der Wert der PV ist eine benannte Zahl, die sich aus dem numerischen Wert der Größe der PV (abgekürzter numerischer Wert der PV) und dem Namen der PV-Einheit zusammensetzt. Beispielsweise ist bei n = 3,8 und [Q] = 1 Gramm die Größe der Masse Q = n [Q] = 3,8 Gramm, bei n = 0,7 und [Q] = 1 Amp. Ist die Größe des Stroms Q = n [Q ] = 0,7 Ampere. Anstelle von "Massegröße ist 3,8 Gramm", "Normalgröße ist 0,7 Ampere" usw., sagen sie und schreiben in der Regel kurz: "Masse ist 3,8 Gramm", die Stromstärke beträgt 0,7 Ampere " usw.
Die PV-Größen werden meistens als Ergebnis ihrer Messung erkannt. Die Messung der Größe von PV (abgekürzt - Messung von PV) ist die empirisch mit Hilfe spezieller technischer Hilfsmittel, Ermittlung des Wertes von PV und Schätzung der Nähe dieses Wertes zu dem Wert, der die Größe dieser PV perfekt widerspiegelt. Der auf diese Weise gefundene Wert von PV wird als nominal bezeichnet.
Die gleiche Größe Q kann durch unterschiedliche Werte mit unterschiedlichen numerischen Werten ausgedrückt werden, abhängig von der Wahl der PV-Einheit (Q = 2 Stunden = 120 Minuten = 7200 Sekunden = 1/12 Tage). Wenn wir zwei verschiedene Einheiten nehmen, können wir Q = n 1 und Q = n 2 schreiben, woher
n 1 / n 2 = /,
das heißt, die numerischen Werte der EF sind umgekehrt proportional zu ihren Einheiten.
Die Tatsache, dass die Größe der PV nicht von der gewählten Einheit abhängt, impliziert die Bedingung der Eindeutigkeit der Messungen. Dies besteht darin, dass das Verhältnis der beiden Werte einer bestimmten PV nicht davon abhängen sollte, welche Einheiten bei der Messung verwendet wurden. Beispielsweise hängt das Verhältnis der Geschwindigkeiten eines Autos und eines Zuges nicht davon ab, ob diese Geschwindigkeiten in Kilometer pro Stunde oder in Metern pro Sekunde ausgedrückt werden. Dieser auf den ersten Blick unveränderliche Zustand konnte bei der Messung bestimmter PVs (Härte, Lichtempfindlichkeit usw.) leider noch nicht beobachtet werden.
1. Theoretischer Teil
1.1 Das Konzept der physikalischen Größe
Gewichtsobjekte der Welt sind durch ihre Eigenschaften gekennzeichnet. Eine Eigenschaft ist eine philosophische Kategorie, die eine solche Seite eines Objekts (Phänomen, Prozess) ausdrückt, die ihre Differenz oder Gemeinsamkeit mit anderen Objekten (Phänomenen, Prozessen) bestimmt und in ihrer Beziehung zu ihnen offenbart. Eigenschaft ist eine Qualitätskategorie. Zur quantitativen Beschreibung verschiedener Eigenschaften von Prozessen und physischen Körpern wird der Begriff der Größenordnung eingeführt. Der Wert ist eine Eigenschaft von etwas, das von anderen Eigenschaften unterschieden und auf die eine oder andere Weise bewertet werden kann, einschließlich quantitativ. Der Wert ist nicht für sich allein vorhanden, sondern nur, sofern ein Objekt vorhanden ist, dessen Eigenschaften durch einen bestimmten Wert ausgedrückt werden.
Durch die Analyse der Werte können wir sie in zwei Typen einteilen (Abb. 1): die Werte des Materialtyps (real) und die Werte idealer Realitätsmodelle (ideal), die sich hauptsächlich auf die Mathematik beziehen und eine Verallgemeinerung (Modell) bestimmter realer Konzepte sind.
Reale Werte sind wiederum in physische und nichtphysische unterteilt. Im Allgemeinen kann eine physikalische Größe als eine Menge definiert werden, die für materielle Objekte (Prozesse, Phänomene), die in den Naturwissenschaften (Physik, Chemie) und in den Ingenieurwissenschaften studiert werden, spezifisch ist. Die nichtphysischen Werte sollten den Werten der sozialen (nichtphysischen) Wissenschaften - Philosophie, Soziologie, Ökonomie usw. - zugeordnet werden.

Abb. 1. Einstufung der Mengen
Das Dokument RMG 29-99 behandelt die physikalische Größe als eine der Eigenschaften eines physischen Objekts, was qualitativ für viele physische Objekte üblich ist, aber quantitativ für jedes Objekt. Individualität wird quantitativ in dem Sinne verstanden, dass eine Eigenschaft für ein Objekt eine bestimmte Anzahl von Malen mehr oder weniger als für ein anderes Objekt sein kann.
Körperliche Größen sollten in messbare und messbare unterteilt werden. Die gemessene PV kann in Form einer bestimmten Anzahl von festgelegten Maßeinheiten quantifiziert werden. Die Möglichkeit, solche Einheiten einzuführen und zu verwenden, ist ein wichtiges Unterscheidungsmerkmal der gemessenen EF. Physikalische Größen, für die aus irgendeinem Grund keine Maßeinheit eingegeben werden kann, können nur geschätzt werden. Unter der Bewertung wird die Zuweisung eines bestimmten Wertes einer bestimmten Anzahl nach festgelegten Regeln verstanden. Der Wert wird anhand von Skalen geschätzt. Die Größenskala ist ein geordneter Satz von Betragswerten, der als Ausgangsbasis für die Messung eines bestimmten Betrags dient.
Nichtphysische Größen, für die die Mengeneinheit grundsätzlich nicht eingegeben werden kann, können nur geschätzt werden. Es ist zu beachten, dass die Schätzung nichtphysikalischer Größen nicht in die Aufgaben der theoretischen Messtechnik einbezogen wird.
Für eine detailliertere Untersuchung der PV müssen die allgemeinen messtechnischen Merkmale ihrer einzelnen Gruppen klassifiziert und identifiziert werden. Mögliche PV-Klassifizierungen sind in Abb. 3 dargestellt. 2
Nach Art der PV-Phänomene werden unterteilt in:
Real, d.h. Mengen, die die physikalischen und physikalisch-chemischen Eigenschaften von Stoffen, Materialien und Produkten beschreiben. Diese Gruppe umfasst Masse, Dichte, elektrischen Widerstand, Kapazität, Induktivität usw. Manchmal werden diese PVs als passiv bezeichnet. Für ihre Messung ist es notwendig, eine Hilfsenergiequelle zu verwenden, mit deren Hilfe das Messinformationssignal erzeugt wird. In diesem Fall werden passive EFs in aktive konvertiert, die gemessen werden.
Energie, d.h. Größen, die die Energieeigenschaften der Umwandlungsprozesse, der Übertragung und der Verwendung von Energie beschreiben. Dazu gehören Strom, Spannung, Leistung und Energie. Diese Werte werden als aktiv bezeichnet.
Sie können ohne Verwendung von Hilfsenergiequellen in Messinformationssignale umgewandelt werden.
Diese Gruppe umfasst verschiedene Arten von Spektraleigenschaften, Korrelationsfunktionen und andere Parameter.
Durch die Zugehörigkeit zu verschiedenen Gruppen physikalischer Prozesse wird PV in Raum-Zeit-, mechanische, elektrische und magnetische, thermische, akustische, Licht-, physikalisch-chemische, ionisierende Strahlung, Atom- und Kernphysik unterteilt.
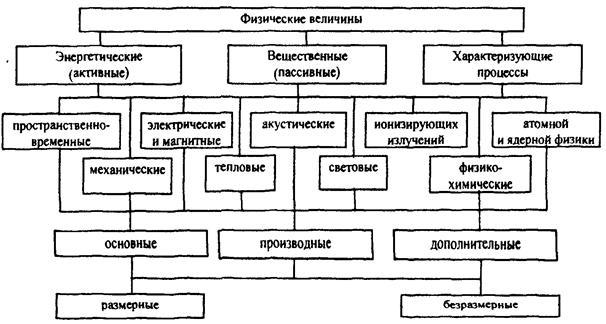
Abb. 2. Klassifizierung der physikalischen Größen
Entsprechend dem Grad der bedingten Unabhängigkeit von anderen Werten dieser Gruppe werden alle PVs in Basis (bedingt unabhängig), Ableitungen (bedingt abhängig) und zusätzlich unterteilt. Gegenwärtig verwendet das SI-System sieben physikalische Größen, die als Hauptgrößen ausgewählt werden: Länge, Zeit, Masse, Temperatur, elektrischer Strom, Lichtstärke und Stoffmenge. Zusätzliche FV umfassen flache und feste Winkel. Durch das Vorhandensein der Dimension werden FV in Dimensionen unterteilt, d.h. Dimension haben und dimensionslos.
1.2 Metrisches Maßsystem
Der Mangel an rationalen Begründungen für die Auswahl der Einheiten von VF führte zu einer großen Vielfalt nicht nur in verschiedenen Ländern, sondern sogar in verschiedenen Orten eines Landes. Dies bereitete insbesondere in den internationalen Beziehungen große Schwierigkeiten. Es entstand ein metrisches Maßsystem, d. empfohlener Satz von PV-Einheiten anstelle von zuvor verwendeten.
Die Einheiten wurden genommen: Länge - Meter (m), Masse - Kilogramm (kg), Volumen - Liter (l), Zeit - Sekunde (s).
Dezimale Vielfache und Untereinheiten von PV wurden ebenfalls eingeführt, d. H., PV-Einheiten waren um das Zehnfache größer und kleiner, und es wurden einfache Regeln für die Zuordnung von Namen zu mehreren und partiellen PV-Einheiten unter Verwendung von Präfixen festgelegt: Kilo, Hekto, Deca, Deci, Centi und milli [zB Zentimeter (cm), Millimeter (mm), Dekaliter (ergeben) usw.]
Dies gab den Einheiten des metrischen Systems (metrische Einheiten von PV) einen erheblichen Vorteil gegenüber den anderen, die zu dieser Zeit existierten. Darüber hinaus erlaubten uns die metrischen Einheiten von PV nicht, zusammengesetzte benannte Zahlen zu verwenden (z. B. die Länge von 8 Faden von 3 Fuß 5 Zoll), und die Berechnungen wurden erheblich vereinfacht.
1.3 Systeme physikalischer Größen
Baueinheiten und Systeme von Einheiten. Bisher wurden Einheiten verschiedener EFs in der Regel unabhängig voneinander installiert. Ausnahmen waren nur Längen-, Flächen- und Volumeneinheiten. Das Hauptmerkmal moderner PV-Einheiten besteht darin, dass sie Abhängigkeiten zwischen ihnen herstellen. In diesem Fall werden mehrere PV-Grundeinheiten willkürlich ausgewählt, und alle anderen abgeleiteten PV-Einheiten werden unter Verwendung von Abhängigkeiten (Gesetzen und Definitionen) erhalten, die verschiedene PVs verbinden, d. H. Gleichungen definieren.
Physikalische Größen, deren Einheiten als die wichtigsten genommen werden, werden als Haupt-PVs bezeichnet, und deren Einheiten sind Derivate, werden als Derivate der PV bezeichnet.
Die Kombination aus grundlegenden und abgeleiteten PV-Einheiten, die alle oder einige Bereiche der Physik abdecken, wird als System von PV-Einheiten bezeichnet.
Betrachten Sie die Beispiele der Festlegung der abgeleiteten PV-Einheiten für die ausgewählte PV als Haupt-PV der Länge L, der Masse M und der Zeit T, d. H. mit ausgewählten Grundeinheiten von VF [L], [M] und [T].
Beispiel 1. Festlegen der Flächeneinheit. Wählen Sie eine einfache geometrische Form, beispielsweise einen Kreis. Die Größe der Fläche s des Kreises ist proportional zum zweiten Grad der Größe ihres Durchmessers d: s = k S d 2, wobei k S der Proportionalitätskoeffizient ist. Diese Gleichung gilt als bestimmender Faktor. Wenn die Größe des Durchmessers des Kreises gleich der Einheit der Länge ist, d. H. D = [L], erhalten wir [s] = k S [L] 2. Die Wahl des Proportionalitätskoeffizienten k S ist beliebig, sei k S = 1, dann sei [s] = [L] 2, d. H. Die Fläche eines Kreises, dessen Durchmesser gleich der Längeneinheit ist, pro Flächeneinheit gewählt. Wenn [L] = 1 m, dann ist [s] = 1 m 2. Die Fläche eines Kreises muss in diesem Fall mit der Formel s = d 2 und die Fläche eines Quadrats mit der Seite b mit der Formel s = (4 / p) b 2 berechnet werden.
Normalerweise wird anstelle einer solchen kreisförmigen Flächeneinheit eine bequemere quadratische Einheit verwendet, bei der es sich um die Fläche eines Quadrats mit einer Seite handelt, die einer Längeneinheit entspricht.
Wenn bei der Erstellung einer kreisförmigen Flächeneinheit angenommen wurde, dass k S = p / 4 ist, dann würde diese mit der üblichen quadratischen Einheit zusammenfallen.
Beispiel 2. Ermittlung der Geschwindigkeitseinheit. Als bestimmenden Faktor nehmen wir die Gleichung an, die zeigt, dass die Größe der Geschwindigkeit und der gleichförmigen Bewegung umso größer ist, je größer die Größe l des durchquerten Pfads ist und je kleiner die auf diesem Pfad aufgewendete Zeit ist T:
dabei ist k u der Proportionalitätskoeffizient.
Mit l = [L], T = [T] erhalten wir die Einheit der Geschwindigkeit [u] = kuku [L] [T] -1. Wenn wir aus Bequemlichkeitsgründen ku = 1 setzen, wird die Geschwindigkeitseinheit [u] = [L] [T] -1 sein. Wenn [L] = 1 mi [T] = 1c gemäß der letzten Formel [u] = 1 m / s ist.
Beispiel 3. Ermittlung der Beschleunigungseinheit. Als definierende Gleichung nehmen wir die Definition der Beschleunigung als eine Ableitung der Geschwindigkeit über der Zeit an: a = du / dT. Mit du = [u], dT = [T] erhalten wir die Einheit der Beschleunigung: [a] = ![]() Mit [L] = 1 m und [T] = 1s [a] = 1 m / s 2.
Mit [L] = 1 m und [T] = 1s [a] = 1 m / s 2.
Beispiel 4. Festlegen der Krafteinheit. Wählen Sie als bestimmende Gleichung des Weltgesetzes
f = wobei m 1 und m 2 die Größen der Körpermassen sind;
r ist die Größe des Abstands zwischen den Zentren dieser Massen;
k f - Verhältnismäßigkeitskoeffizient.
Wenn man m 1 = m 2 [M] setzt, r = [L], erhalten wir die Einheit der Kraft
![]()
oder wenn k f = 1 [f] = [M] 2 [L] -2 ist. Mit [L] = 1 m und [M] = 1 kg gemäß der letzten Formel [f] = 1 kg 2 / m 2.
Wenn wir als Bestimmungsgleichung für das zweite Newtonsche Gesetz f = = kf ma wählen, erhalten wir ähnlich wie in der vorherigen Einheit die Kraft in der Form [f] = kf [M] * [a] = kf [M] [L] [T] -2 oder in der Form [f] = [M] [L] [T] -2. Mit [M] = 1 kg ist [L] = 1 m und [T] = 1 s gemäß der letzten Formel [f] = 1 kg m / s 2.
Beide empfangenen Einheiten sind gleich, aber die zweite ist weit verbreitet, und die erste wird nur selten verwendet (hauptsächlich in der Astronomie).
Aus den betrachteten Beispielen ist ersichtlich, dass bei den ausgewählten Haupt-PVs - der Länge L, der Masse M und der Zeit T - die abgeleitete Einheit [x] einiger PV durch die Einheiten [L], [M] und [T] nach folgender Formel angeordnet ist:
[x] = k x [L] pL [M] pM [T] pT,
wobei k x - beliebig gewählter Proportionalitätskoeffizient;
p L, p M und p T sind positive oder negative Zahlen.
Diese Zahlen zeigen, wie die abgeleitete Einheit der PV mit der Haupteinheit variiert. Beispielsweise ändert sich bei einer Änderung der Basiseinheit [L] q mal die abgeleitete Einheit [x] q pL mal. Da kx die Änderung von [x] nicht beeinflusst, wird der Charakter der Änderung der Einheit [x] mit der Änderung der Einheiten [L], [M] und [T] normalerweise unter Verwendung von Dimensionsformeln ausgedrückt, in denen kx = 1 ist Die Dimensionsformel lautet
dimx = LpLMpLTpT,
wo die rechte Seite als Dimension der PV-Einheit bezeichnet wird; der linke Teil - die Bezeichnung dieser Dimension (Dimension);
p L, p M und p T sind die Indikatoren der Dimension.
Dies ist aus der Dimensionsformel auf dieselbe Weise ersichtlich, wie sich die Größe der PV-Ableitung mit einer Änderung der Größe der Haupt-PV für die gewählte Definitionsgleichung ändert. Die rechte Seite dieser Formel wird als Dimension der FW bezeichnet.
Betrachten Sie den allgemeinen Fall, wenn es mehrere Basis-PVs A, B, C, D, ... gibt, deren Einheiten [A], [B], [C], [D], ... sind. Dann offensichtlich die Ableitung der Ableitung Die Einheiten des PV x werden auf die Wahl einer endgültigen Gleichung reduziert, die x mit anderen (Basis- und Ableitungs-PVs) in Beziehung setzt, um diese Gleichung in die Form zu bringen:
x = k x A pA B pB C pC D pD ...,
wobei p A, p B, p C, p D, ... Indikatoren für die Dimension sind und die Haupt-EF durch ihre Einheiten zu ersetzen:
[x] = k x [A] pA [B] pB [C] pC [D] pD ...
Die Formel für die Dimension lautet in diesem Fall:
dim x = A pA B pB C pC D pD ...
Es ist bekannt, dass die abgeleitete Einheit FV x die Abmessung p A relativ zur Basiseinheit FV A, die Abmessung p B relativ zur Basiseinheit FV B usw. hat. (oder dass die Ableitung des PV die Dimension p A relativ zum Haupt-PV A hat, die Dimension p B relativ zum Haupt-PV B usw.). Wenn wir die Dimension der Geschwindigkeit (Beispiel 2) LT -1 oder L 1 M 0 T -1 betrachten, können wir also sagen, dass die Geschwindigkeit die Dimension 1 relativ zur Länge, die Dimensionen der Dimension 0 relativ zur Masse und die Dimension 1 relativ zur Zeit hat (die Geschwindigkeit der Einheit hat die Dimension 1 relativ zu 1) Längeneinheiten usw.).
Wenn p A = p B = p C = p D = ... = 0 ist, wird die Ableitung von PV x als dimensionsloses PV bezeichnet, und ihre Einheit [x] wird als dimensionslose Einheit von PV bezeichnet.
Ein Beispiel für eine dimensionslose Ableitung einer PV-Einheit ist die Einheit [φ] eines flachen Winkels φ - Radian. Wenn diese Einheit als die entscheidende Einheit festgelegt wird, wird die Gleichung φ = = k φ (l / r) angenommen, was anzeigt, dass der Winkel φ größer ist, je größer die Länge von l ist, ihr Bogen und je kleiner die Länge der Länge r des Radius dieses Bogens. In der Gleichung gilt k = 1, l = [L], r = [L]. Daher gilt [φ] = = [L] 0 und dim φ = L 0.
Wenn beim Festlegen der abgeleiteten Einheit der PV in ihren Ausdrücken durch die Basiseinheiten der PV k x = 1 angenommen wird, wird sie als kohärente abgeleitete Einheit der PV bezeichnet. Das System von PV-Einheiten, von denen alle abgeleiteten Einheiten kohärent sind, wird als zusammenhängendes System von PV-Einheiten bezeichnet.
Die Abmessungen der abgeleiteten Einheiten von PV x, y und z sind wie folgt miteinander verbunden. Wenn z = k 1 xy ist, dann
dimz - dimx * dimu. (1.2)
Wenn z = k 2 ist
dimz - dimx / dimu. (1.3)
Wenn z = k 3 x n ist, dann
dimz - (dimx) n. (1.4)
Gleichungen (1.2) und (1.3) wurden zur Bestimmung der Einheiten Beschleunigung und Kraft verwendet, und Gleichheit (1.4) ist eine Folge von Gleichheit (1.2).
Dimensionsformeln können nur für solche EF geschrieben werden, deren Messung die Bedingung der Eindeutigkeit der Messungen erfüllt. Die Abmessungen verschiedener EF können zusammenfallen (z. B. Kraft- und Arbeitsmomente), und die Abmessungen derselben EF in verschiedenen Systemen von EF-Einheiten können unterschiedlich sein (siehe Beispiel 4, wo unterschiedliche Definitionsgleichungen zu unterschiedlichen Abmessungen der Krafteinheiten führten und daher unterschiedliche Kraftdimensionen). Daher geben die Abmessungen kein vollständiges Bild der PV. Die Diskrepanz zwischen den Abmessungen der linken und rechten Seite einer Formel oder einer Gleichung zeigt jedoch die Fehlerhaftigkeit dieser Formel oder dieser Gleichung an. Darüber hinaus erleichtert das Dimensionskonzept die Lösung vieler Probleme. Wenn bereits bekannt ist, welche PVs in den untersuchten Prozess involviert sind, ist es möglich, mithilfe der Dimensionsanalyse die Art der Beziehung zwischen den Dimensionen dieser PVs zu bestimmen. In diesem Fall ist die Lösung des Problems oft viel einfacher, als wenn es auf andere Weise durchgeführt würde.
Bezeichnenderweise mit der mathematischen Formulierung physikalische Phänomene Unter FV-Symbolen bedeuten sie nicht die FV selbst und nicht ihre Größe, sondern die Werte der FV, dh benannten Zahlen. Zum Beispiel sind in der Gleichung f = kf ma, die Newtons zweiten Satz ausdrückt, unter den Symbolen t und a nicht die PV selbst (Masse und Beschleunigung) und nicht die Abmessungen von Masse und Beschleunigung, die nicht miteinander multipliziert werden können, sondern die Werte von Masse und Beschleunigung t gemeint. Benannte Zahlen, die die Abmessungen der Masse und der Beschleunigung widerspiegeln und für die die Multiplikation sinnvoll ist.
1.4 Einheitensysteme
Das erste System von PV-Einheiten bestand im Wesentlichen aus den oben genannten metrischen PV-Einheiten. Erst im Jahr 1832 schlug K. Gauss jedoch vor, Anlagen aus PV-Einheiten als Kombination aus Basis- und abgeleiteten Einheiten zu bauen. In dem von ihm gebauten System waren die Basiseinheiten von PV Millimeter, Milligramm und Sekunde.
Später tauchten andere Systeme von PV-Einheiten auf, die ebenfalls auf metrischen PV-Einheiten basierten, jedoch mit unterschiedlichen Basiseinheiten. Die bekanntesten dieser Systeme sind folgende.
GHS-System (1881). Die Basiseinheiten von PV sind Zentimeter, Gramm, Sekunde. Das System ist in der Physik sehr verbreitet geworden. Später wurden einige Varianten dieses Systems für elektrische und magnetische PV entwickelt.
Das System von MTS (1919). Grundeinheiten von PV-Meter, Tonne (1000 kg), Sekunde. Dieses System wurde nicht weit verbreitet.
ICSS-System ( ende von XIX in). Grundeinheiten von PV - Meter, Kilogrammkraft, Sekunde. Dieses System ist im Engineering weit verbreitet.
System MKSA (1901). Es wird manchmal das Georgie-System (nach seinem Schöpfer) genannt. Die Basiseinheiten von PV sind Meter, Kilogramm, Sekunde und Ampere. Dieses System ist derzeit angemeldet. teil von im neuen internationalen Einheitensystem von PV.
Alle Basiseinheiten und abgeleiteten Einheiten eines Systems von PV-Einheiten werden Systemeinheiten von PV genannt (in Bezug auf dieses System). Neben den Systemeinheiten gibt es auch sogenannte Nichtsystemeinheiten, d. H. Solche, die nicht in dem System von PV-Einheiten enthalten sind. Alle PV-Einheiten außerhalb des Systems können in zwei Gruppen unterteilt werden: 1) nicht in einem der bekannten Systeme enthalten, zum Beispiel: Längeneinheit - X-Einheit, Druckeinheit - Millimeter Quecksilbersäule, Energieeinheit - Elektronenvolt; 2) nur in Bezug auf einige Systeme nicht systemisch sein, zum Beispiel: Längeneinheit - Zentimeter - nicht systemisch für alle Systeme außer GHS; Masse-Ton-Off-System für alle Systeme außer MTS; Die elektrische Kapazitätseinheit - Zentimeter - ist für alle Systeme außer CGSE außerhalb des Systems.
Das Vorhandensein verschiedener Systeme von PV-Einheiten sowie einer großen Anzahl von Off-System-PV-Einheiten schafft Unannehmlichkeiten, die mit den Berechnungen verbunden sind, die beim Wechsel von einer PV-Einheit zu einer anderen erforderlich sind. Im Zusammenhang mit dem Wachstum der wissenschaftlichen und technischen Beziehungen zwischen den Ländern wurde die Vereinheitlichung der PV-Einheiten erforderlich. Als Ergebnis wurde ein neues Internationales System von VF-Einheiten geschaffen.
Das internationale Einheitensystem. 1960 wurde die XI. Generalkonferenz für Maße und Gewichte gebilligt Internationales System Einheiten von PV SI ·.
In der UdSSR und in den Ländern - Mitgliedern der CMEA - wurde SI in den Standard der CMEA STSEV 1052 - 78 "Metrology eingeführt. Einheiten der physikalischen Größen "Informationen zu den Basiseinheiten der PV-SI sind in der Tabelle angegeben. 1
Zwei im Wesentlichen abgeleitete Einheiten des PV SI: Eine flache Winkeleinheit - Radiant (russische Bezeichnung ist glücklich, international - rad) und eine Raumwinkeleinheit - Steradisch (russische Bezeichnung cp, international - sr) - werden nicht offiziell abgeleitet und werden als zusätzliche Einheiten des PV SI bezeichnet . Der Grund für ihre Isolierung ist, dass sie durch die Definitionsgleichungen j = l / r und y = S / R 2 festgelegt werden, wobei j ein flacher Winkel ist, dessen Scheitelpunkt mit dem Mittelpunkt des Bogens der Länge l und dem Radius r zusammenfällt; y ist der Raumwinkel, dessen Scheitelpunkt mit dem Mittelpunkt einer Kugel mit dem Radius R übereinstimmt und der eine Fläche S auf der Oberfläche der Kugel schneidet
[j] = 0 und [y] = 
dimensionslos und hängen daher nicht von der Wahl der Basiseinheiten der PV-Anlage ab.
Die abgeleiteten Einheiten des PV-SI werden aus den Basis- und weiteren Einheiten gemäß den Regeln für die Bildung kohärenter PV-Einheiten gebildet.
Grundeinheiten der physikalischen Größen SI Tabelle 1.

Zum Beispiel: Winkelbeschleunigung - Quadratmeter im Quadrat (rad / s 2), magnetische Feldstärke - Ampere pro Meter (A / m), Helligkeit - Candela pro Quadratmeter (cd / m 2).
Die Einheiten von PV SI mit speziellen Namen sind in der Tabelle angegeben. 2
Das internationale System hat folgende Vorteile gegenüber anderen Systemen von VF-Einheiten: Es ist universell, d. H. Es deckt alle Bereiche der Physik ab; kohärent; Ihre PV-Einheiten sind in den meisten Fällen praktisch und wurden früher weit verbreitet.
Einheiten, die zur Verwendung in den CMEA-Ländern zugelassen sind. Die oben genannten Vorteile von SI als Ganzes gestatten nicht die Feststellung, dass die EF-Einheiten in allen Fällen akzeptabler sind als andere. Um beispielsweise große Zeiträume zu messen, können der Monat und das Jahrhundert günstigere Einheiten sein als eine Sekunde. Für das Messen großer Entfernungen können ein Lichtjahr und ein Parsec-Wert bequemere Einheiten sein als ein Messgerät usw.
Ableitungen physikalischer Größen SI mit besonderen Namen. Tabelle 2

2. Berechnungsteil
Aufgabe. Mit einem Voltmeter der Genauigkeitsklasse 4, U n = 150 V wurde das Ergebnis der Beobachtung X = 100 V erhalten. Bestimmen Sie den Bereich, in dem sich der wahre Wert befindet, der relative und der absolute Fehler.
Die Entscheidung k = 
Relativer Fehler: 
Wahrer Wert: X und = (100 ± 6) V.
Alle technologischen Aktivitäten des Menschen stehen im Zusammenhang mit der Messung verschiedener physikalischer Größen.
Ein Satz physikalischer Größen ist ein System, in dem einzelne Größen durch ein Gleichungssystem miteinander verbunden sind.
Für jede physikalische Größe muss eine Maßeinheit festgelegt werden. Eine Analyse der Zusammenhänge physikalischer Größen zeigt, dass es unabhängig voneinander möglich ist, Maßeinheiten nur für wenige physikalische Größen festzulegen und den Rest durch diese auszudrücken. Die Anzahl unabhängig festgelegter Werte ist gleich der Differenz zwischen der Anzahl der im System enthaltenen Mengen und der Anzahl unabhängiger Gleichungen der Beziehung zwischen den Mengen.
Wenn zum Beispiel die Geschwindigkeit eines Körpers durch die Formel v = L / t bestimmt wird, können nur zwei Werte unabhängig voneinander eingestellt werden, und der dritte kann in Form von Werten ausgedrückt werden.
Physikalische Größen, deren Einheiten unabhängig von den anderen eingestellt werden, werden als Grundgrößen und ihre Einheiten als Grundeinheiten bezeichnet.
Die Dimension einer physikalischen Größe ist ein Ausdruck in Form eines Potenzmonoms, das sich aus den Produkten von Symbolen der grundlegenden physikalischen Größen in verschiedenen Graden zusammensetzt und die Beziehung dieser Größe zu den in diesem System verwendeten physikalischen Größen von Quantitäten mit einem Proportionalitätskoeffizienten von eins widerspiegelt.
Die Grade der Symbole der Grundgrößen in einem Monom können ganzzahlig, gebrochen, positiv und negativ sein. Gemäß der internationalen Norm ISO 31/0 sollte die Dimension der Werte mit dim angegeben werden. Im LMT-System beträgt die Dimension von X:
dimX = L lMMTt,
wobei L.M.T - Symbole von Werten sind, die als Haupt (jeweils Länge, Masse, Zeit) betrachtet werden;
l, m, t - ganze oder gebrochene, positive oder negative reelle Zahlen, die Indikatoren für die Dimension sind.
Die Dimension einer physikalischen Größe ist mehr als allgemeines Merkmalals der definierende Wert der Gleichung, da Größen mit einer anderen qualitativen Seite inhärent sein können.
Zum Beispiel wird die Arbeitskraft F durch die Gleichung A = Fl bestimmt; Die kinetische Energie eines sich bewegenden Körpers ist die Gleichung E k = mv 2/2, und die Abmessungen beider sind gleich.
Über den Dimensionen kann man Multiplikation, Division, Potenzierung und Wurzelextraktion erzeugen.
Ein Indikator für die Dimension einer physikalischen Größe ist ein Indikator für den Grad, in dem die Dimension der physikalischen Basisgröße aufgebaut wird, die in der Dimension der Ableitung der physikalischen Größe enthalten ist.
Dimensionen werden häufig zur Bildung abgeleiteter Einheiten und zur Überprüfung der Homogenität von Gleichungen verwendet. Wenn alle Exponenten der Dimension Null sind, wird diese physikalische Größe als dimensionslos bezeichnet. Alle relativen Werte (das Verhältnis von ähnlichen Werten) sind dimensionslos.
Physikalische Größe (PV) ist eine Eigenschaft, die für viele physische Objekte qualitativ gleich ist (ihre Zustände und Prozesse, in denen sie vorkommen), für jedes Objekt jedoch quantitativ individuell ist.
Qualitativ gebräuchliche Eigenschaften sind durch die Herkunft von PV gekennzeichnet. Qualitativ häufig können verschiedene (unterschiedliche) PVs im Namen sein: entweder Länge, Breite, Höhe, Tiefe, Entfernung oder elektromotorische Kraft, Spannung, elektrisches Potential oder Arbeit, Energie, Wärmemenge. Man sagt, solche FVs seien gleichartig oder homogen. Nicht homogene physikalische Größen werden als heterogen oder inhomogen bezeichnet.
Quantitativ individuelles Objekt wird durch die Größe der PV charakterisiert. Zum Beispiel sind Geschwindigkeit, Temperatur und Viskosität Eigenschaften, die verschiedenen Objekten innewohnen, aber einige Objekte dieser Eigenschaft haben mehr, andere weniger. Folglich ist die Größe von Geschwindigkeit, Temperatur und Viskosität einiger physischer Objekte größer als die von anderen.
LISTE DER BENUTZTEN LITERATUR
1. Kusnezow V. A., Yalunina G. V. Grundlagen der Messtechnik. Studienführer. - M .: Izd. Standards, 1995. - 280 p.
2. Pronenko V.I., Yakirin R.V. Messtechnik in der Industrie. - Kiew: Technik, 1979. - 223 S.
3. Laktionov BI, Radkevich Ya.M. Messtechnik und Austauschbarkeit. - M .: Verlag der Moskauer Staatlichen Bergbauuniversität, 1995. - 216 p.
Richtiger wäre es, "dimensionslose Einheit der PV" zu sagen, da Dimension nicht Größe, sondern gleich Null ist. Der Begriff "dimensionslose PV-Einheit" ist jedoch weit verbreitet. Gleiches gilt für den Begriff "dimensionsloses PV".
CGSE ist eine der Varianten des CGS-Systems.
· SI steht für Systeme International. Anstelle von SI können Sie SI (System International) schreiben.
